
為什麼數學難學呢?
數學是許多學生的惡夢,很多人在學習中都遭遇過挫折,到底是什麼原因讓數學那麼難呢? 這篇文章將帶你揭開數學困難的面紗,藉由了解數學的特色,改善數學成績。在討論前,先說明兩個前提:
- 學習方式需要因人調整:每個人的學習方法、讀書習慣、困境遭遇點都不同,我們只能廣泛性的說明問題,實際應用時需要根據個人狀況調整。
- 階段不同、方法不同:在求學不同的時期,數學的學習目標並不相同:小學要求運算能力、中學要求簡易抽象化與應用能力、高中要求抽象理解與統合能力、大學以後則需要純粹的抽象化與邏輯推論能力,雖然都是數學,但是不同階段面臨的困難與目標並不一樣,自然需要不同的學習技巧,也因此國中數學好壞,並不能代表未來學習數學的表現。
除此之外,如果只會沿用以前的學習方式,新的階段時很容易就不適應。你需要隨時調整學習的心態與方向。例如:國小依靠大量練習來維持數學成績,到國中這個方法的效率驟減,高中只靠練習題幾乎沒有幫助。

這篇文章聚焦在如何有效的學習數學,不只是單純地要求學生提升練習量,而是假設學生有心要學習、並且練習量充足的條件下,如何更深入且更有效率的面對數學。
學習數學的困難點
1. 不習慣符號化的思維習慣:
國小升上國中時,數學開始使用『代數』這種抽象概念,對學生來說,是一個很大的改變,以前可以確切表示的數字,忽然離開了現實的生活,變成了純粹的符號。這個變化也正是國中生學習數學最先面臨到的障礙,不少國一學生就是不懂 “X” 到底是什麼,因此學的一頭霧水。甚至影響到未來學習數學的信心。
其實,學生是被大量瞬間出現的代數搞混了,如果習慣從題目開始學習,沒有先把代數的性質理解清楚,很容易導致在題目當中看到 “X” 時就混亂了,學生不明白為甚麼一下子 X=1 一下子 X=5。終歸到底,學生的困難在於,不理解代數表達的是『未知』,只是用來處裡還不知道的概念。所以,在學習數學前,優先理解數學符號化的本意,才有辦法把後續包含大量符號化觀念的課程學好。
2. 缺乏抽象歸納與類推習慣:
代數與符號化是學習最基本的理解,當學生能夠認清代數的意義以後,才算具備基本抽象化思考的能力。接下來將會面臨的門檻是:從題目歸納核心邏輯的技巧,以及類推一個觀念到其他題目上使用的習慣,如果缺乏這兩種能力,就會發生花費大量時間練習同一類型的題目,雖然好像很用功,但數學成績卻沒有起色的狀況。這是因為,數學只靠練習題目是不夠的,題型百百種,根本不可能練習完所有的題型,靠練習頂多掌握基礎題型的分數而已,進階變化題根本掌握不完。

跨越這個門檻,就可以脫離只靠練習題學數學的窘境,學會了解題型架構,掌握了核心的邏輯來面對其他題型。運用這種方法,只需要少量的練習,就可以利用找出的邏輯來解決不同變化的題目。
這種歸納類推能力需要練習,接觸到相同的邏輯時,要試著把邏輯剝離原本的事物,變成一個通用性的法則,之後依據這個法則應用於其他事物。其實這樣的思考方式不只適用於學數學,生活上有許多事情都可以用這個方法掌握。這也是為甚麼有些人學習東西特別快的原因,因為他沿用了其他領域的經驗,把原本領域的經驗抽象歸納成基本邏輯,一旦遇到類似的事情時就可以套用,自然很快就會上手。這裡舉個簡單的數學題目,來說明對題目做到提出核心邏輯:
假設有一個農場,雞的數目是鴨的四倍,豬比鴨少九隻。鴨和豬的數目是六十七隻。請問農場所有動物的腳加起來共多少隻?
這是一個很經典的農場問題,解法非常簡單,只需要讓 “鴨=X” 就可以快速解出答案:
鴨=X 雞=4X 豬=X-9 且(X)+(X-9) = 67 則X=38 …
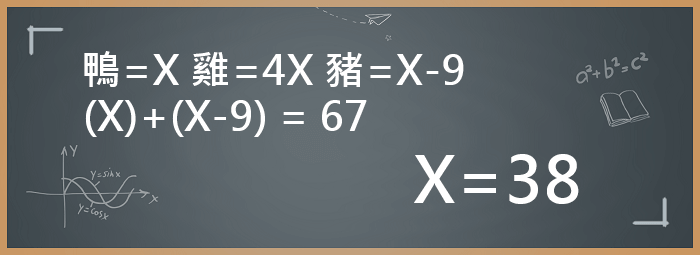
但是我們可以進一步去思考題目的變化,以抽出代數考題的核心邏輯。試想如果把 “鴨=X”,換成 “雞=X”會發生什麼事情呢?這時候:
鴨=X/4 雞=X 豬=(X/4)-9 且(X/4)+(X/4-9) = 67 …
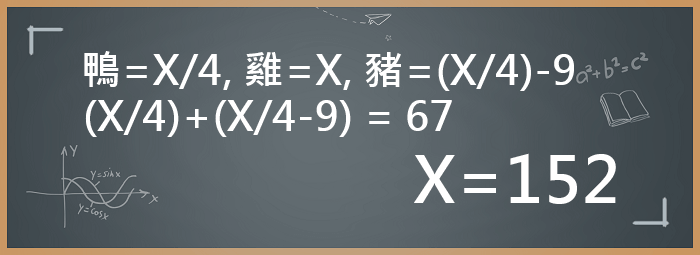
算式一樣可以計算,但是難度卻提高不少,與前面的方法相比,更容易造成運算錯誤。這說明了代數題目的一個特點,選對未知數對於計算會有很大的幫助。在不知道該怎麼選的時候應該多嘗試用不同的代數。
再來,我們還可以用多個代數表示這個問題:
鴨=X 雞=Y 豬=Z Y=4X Z=X-9 X+Z=67
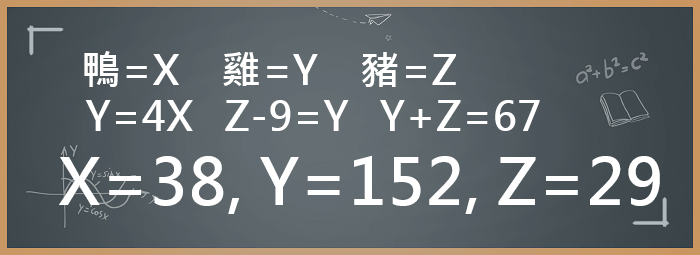
依然可以求解,只是又更複雜了,而這個經驗說明代數問題的另一個現象:如果條件允許,盡可能地減少代數數量,對於計算很有幫助。
實際上每個題目都可以做這樣的延伸技巧,針對不同的題目做這種思想演練,很快就會發現題目其實只是在一些基本原則上做變化而已,本質上要考的內容都是類似的。例如:圖形題總是在邊長、面積、角度、相似性上做變化;代數題關鍵是簡化運算、找出適合當代數的目標…等等。掌握這些題型的原理才是練習題目最重要的,如果不動腦筋的只是大量練習,很快就會在數學上面臨挫敗感。
掌握考題重點,是事半功倍的學習技巧
3.缺乏統整經驗:
如果解決了上述的兩個問題,並且輔以足夠的練習量,數學成績就不會差了,但是離頂尖還有一步之遙,那就是非常困難的變化題,常常會想不到解法。這需要藉由調整數學各單元的整合能力,來強化對難題的處理能力。
數學是一個有完整系統的學科,擁有非常強的連貫性,以前學過的東西在未來章節會不斷出現,例如:線性代數的觀念會應用於座標圖型、幾何學用於空間…等等。不過在教學時必須把數學切割成多個學習環節,可也正是這樣的方法讓學生容易產生盲點,以為解圖型時不會用到代數、解代數時不會需要畫圖…等等,缺少整合性的觀念,就會在遇到跨章節的整合題目時找不到解法。

因此,建議學生可以把過往學過的公式與定理重新整理,試著將整個數學觀念融會貫通,一旦遇到不知道怎麼解決的題目時,只需要把曾經學習過的東西都條列出來,幾乎都可以在其中找到需要的公式與想法,例如:題目有三角形時就可以列出畢氏定理、相似性、中點、重心、外接圓…等等,透過把學習過的觀念打散重新組裝,讓數學觀念一氣呵成,是晉升頂尖很好的方式。
4.定勢效應的影響:
最後來討論一個在考試時,特別常見的問題,很多考生在考試當下解不出來的題目,一離開考場反而就想到解法了。其實這種狀況在心理學有相當多的研究,最著名的理論為『定勢效應』。
定勢效應指的是大腦傾向採用熟悉的方法來解決問題,並頑固的忽視其他方法,甚至是更好的方法。在1942年的一項經典實驗中,美國心理學家路琴(Abraham Luchins)要求受試者做了一個假想實驗,實驗的邏輯大致如下:
請大家假想自己需要用倒水的方式來解決簡單的數學問題。首先,你手上有三個水杯,容量分別為21、127、3,請試著倒出100單位的容量,條件是每次盛裝或倒出的水量都必須是這三個容器的容量之一,不能任意倒,而操作次數並沒有限制。
這個問題並不困難,只需要如下操作:
先裝滿127的水杯,倒給21一次、接著倒給3兩次,這樣就得到100單位的水了

那麼現在請大家接著思考以下這幾個數字:
題目:23、70、7目標是40 下一題:93、44、3目標是40 最後一題23、49、3目標是20。

有趣的問題來了,請問各位的最後一題是怎麼解決的? 實驗證明多數的人採用的方法如下:49-23=26,26在倒兩次3得到20,看起來很合理,可是最後一題其實只需要用23倒掉3就夠了,根本不用經過中間的49單位。
這項水杯實驗是『定勢效應』(Einstellung effect)的相關研究中,最為人所知的實驗之一。這個效應指出人們在解決問題時傾向採用熟悉的方法,通常是最先想到的方法,而且這個方法會一直盤踞心中,並使人忽視其他可能的方法。
延伸資料:定勢效應 – 維基百科
考試時學生也很容易受到定勢效應的影響,由於第一印象想要用的方法失敗了,導致想法卡住而沒辦法抽離,在考試當中由於有時間壓力,讓人更難以跳脫思維。對於考試來說,最好的方法是一旦被某個題目困住了,就往下繼續做,不要花時間在題目上糾結,因為定勢效應已經讓思維固定了,花更多時間也不一定能夠找出好的解法,反而會浪費考試時間,增加考試壓力,不如先做別的題目轉換思路,顯得更有機會解決問題。

這篇文章總結了國中數學容易遇到的困難,由基本問題到進階的困境,正確理解並實踐絕對可以改善學生數學的學習效率。希望大家都可以逐步克服學習數學的障礙,保持積極與自信的學習態度。


數學不會就是不會,只要會加減乘除即可,學那麼多未來也不會用到,倒不如不要學,去學自己有興趣的科目比較重要。
好可憐喔
很有啟發性的文章。